So let see if I got this...
Photons are particles much smaller than atoms. The more photons a lamp shoots off, the brighter the light. Light is a form of energy that behaves like the waves in water or radio waves. The distance between the top of one wave and the top of the next wave is called a 'wavelength.' Each photon carries a certain amount, or 'quantum', of energy depending on its wavelength.
Black at left is
ultraviolet (high frequency); black at right is
infrared (low frequency).
A light's color depends on its wavelength. The color violet (the bottom or innermost color of the rainbow) has a wavelength of about 400 nm ("nanometers") which is 0.00004 centimeters or 0.000016 inches. Photons with wavelengths of 10-400 nm are called ultraviolet (or UV) light. Such light cannot be seen by the human eye. On the other end of the spectrum, red light is about 700 nm. Infrared light is about 700 nm to 300,000 nm. Human eyes are not sensitive to infrared light either.
Wavelengths are not always so small. Radio waves have longer wavelengths. The wavelengths for your FM radio can be several meters in length (for example, stations transmitting on 99.5 FM are emitting radio energy with a wavelength of about 3 meters, which is about 10 feet). Each photon has a certain amount of energy related to its wavelength. The shorter the wavelength of a photon, the greater its energy. For example, an ultraviolet photon has more energy than an infrared photon.

Pictorial description of frequency
Wavelength and frequency (the number of times the wave crests per second) are inversely proportional. This means a longer wavelength will have a lower frequency, and vice versa. If the color of the light is infrared(lower in frequency than red light), each photon can heat up what it hits. So, if a strong infrared lamp (a heat lamp) is pointed at a person, that person will feel warm, or even hot, because of the energy stored in the many photons. The surface of the infrared lamp may even get hot enough to burn someone who may touch it. Humans cannot see infrared light, but we can feel the radiation in the form of heat. For example, a person walking by a brick building that has been heated by the sun will feel heat from the building without having to touch it.
The mathematical formulations of quantum mechanics are abstract. A mathematical function, the wavefunction, provides information about the probability amplitude of position, momentum, and other physical properties of a particle. Many of the results of quantum mechanics are not easily visualized in terms of classical mechanics.
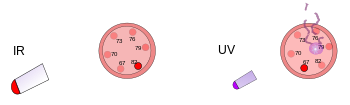
On the left, a plastic thermometer is under a bright heat lamp. This infrared radiation warms but does not damage the thermometer. On the right, another plastic thermometer gets hit by a low intensity ultraviolet light. This radiation damages but does not warm the thermometer.
If the color of the light is ultraviolet (higher in frequency than violet light), then each photon has a lot of energy, enough to hurt skin cells and cause a sunburn. In fact, most forms of sunburn are not caused by heat; they are caused by the high energy of the sun's UV rays damaging your skin cells. Even higher frequencies of light (or electromagnetic radiation) can penetrate deeper into the body and cause even more damage. X-rays and gamma rays have so much energy that they can go deep into the human body and kill cells. Humans cannot see or feel ultraviolet light, x-rays or gamma rays. They may only know they have been under such high frequency light when they get a radiation burn. Areas where it is important to kill germs often use ultraviolet lamps to destroy bacteria, fungi, etc. X-rays and gamma rays are sometimes used to kill cancer cells.
Quantum mechanics started when it was discovered that a certain frequency means a certain amount of energy. Energy is proportional to frequency (E ∝ f). The higher the frequency, the more energy a photon has, and the more damage it can do. Quantum mechanics later grew to explain the internal structure of atoms. Quantum mechanics also explains the way that a photon can interfere with itself, and many other things never imagined in classical physics.
Max Planck discovered the relationship between frequency and energy. Nobody before had ever guessed that frequency would be directly proportional to energy (this means that as one of them doubles, the other does, too). If we choose to use what are called natural units, then the number representing the frequency of a photon would also represent its energy. The equation would then be:
E = f
meaning energy equals frequency.
But the way physics grew, there was no natural connection between the units then used to measure energy and the units commonly used to measure time (and therefore frequency). So the formula that Planck worked out to make the numbers all come out right was:
E =
h × f
or, energy equals
h times frequency. This
h is a number called Planck's constant after its discoverer.
Quantum mechanics is based on the knowledge that a photon of a certain frequency means a photon of a certain amount of energy. Besides that relationship, a specific kind of atom can only give off certain frequencies of radiation, so it can also only give off photons that have certain amounts of energy.
The particle in a 1-dimensional well is the most simple example showing that the energy of a particle can only have specific values. The energy is said to be "quantized." The well has zero potential energy inside a range and has infinite potential energy everywhere outside that range. For the 1-dimensional case in the {\displaystyle x}
direction, the time-independent Schrödinger equation can be written as:
[5]
{\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi .}
Using differential equations, we can see that {\displaystyle \psi }
must be
{\displaystyle \psi =Ae^{ikx}+Be^{-ikx}\;\;\;\;\;\;E={\frac {\hbar ^{2}k^{2}}{2m}}}
or
{\displaystyle \psi =C\sin kx+D\cos kx\;}
(by Euler's formula)
The walls of the box mean that the wavefunction must have a special form. The wavefunction of the particle must be zero anytime the walls are infinitely tall. At each wall:
{\displaystyle \psi =0\;\mathrm {at} \;\;x=0,\;x=L}
Consider
x = 0
- sin 0 = 0, cos 0 = 1. To satisfy {\displaystyle \scriptstyle \psi =0\;}
the cos term has to be removed. Hence D = 0
Now consider: {\displaystyle \scriptstyle \psi =C\sin kx\;}
- at x = L, {\displaystyle \scriptstyle \psi =C\sin kL=0\;}
- If C = 0 then {\displaystyle \scriptstyle \psi =0\;}
for all x. This solution is not useful.
- therefore sin kL = 0 must be true, giving us
{\displaystyle kL=n\pi \;\;\;\;n=1,2,3,4,5,...\;}
We can see that {\displaystyle n}
must be an integer. This means that the particle can only have special energy values and cannot have the energy values in between. This is an example of energy "quantization."
-----------------------------------------------------------------------------------------------------------
Naaa... ha ha ha
That still don't make sense at all...
But it shore looked like I was really smart for a wile right, typing up all that text :nerd:
:stuck_out_tongue_winking_eye: :joy::joy::joy::joy::joy:
CHEERS!
:beer::beer::beer::beer::beer::beer::beer::beer::beer::beer:
:beers::beers::beers::beers::beers::beers::beers::beers::beers::beers::beers: